Главная Пишите

Арифметика и теория чисел

Хорошая теория – самая практичная вещь на свете. Начало арифметики относится к незапамятной древности. Изобретение десятичной системы и цифр приписывается индусам, халдейцам, финикянам, египтянам [и майя]. Первыми учеными, писавшими об арифметике, были греки Евклид, Диофант, Эратосфен и др. Арабы, усвоившие труды греческих математиков, развили далее науку арифметики и познакомили с ней европейцев в IX в. Арабские (собственно индийские) цифры стали известны в Европе в 13-м веке (дотого в употреблении были лишь римские). Региомонтанус (XV в.) ввел десятичные дроби [они использовались уже египтянами]. Развитию арифметики способствовали в Европе: Пейрбах, Региомонтанус, Пачиоли, Стифель, Хр. Вольф, Эйлер, Лейбниц, Паскаль, Фермат. (Малый энциклопедический словарь Брокгауза и Ефрона) Арифметика (греч.) - часть математики, которая занимается изучением некоторых свойств чисел, выраженных цифрами, и действиями над ними. В более широком смысле арифметика определяется как наука о свойствах чисел вообще, причем различают простую и общую арифметику, низшую и высшую арифметику. В  простой арифметике занимаются определенными числами, то есть выраженными цифрами. В общей арифметике, иначе алгебре, вместо цифр употребляются буквенные знаки [переменные], то есть, алгебра есть обобщенная арифметика. Для удобства в педагогическом отношении более сложные части арифметики: возвышение в степень, извлечение корня, решение задач с уравнениями также переносят в курс алгебры.

В  низшую арифметику входят:

• четыре основных действия (сложение, вычитание, умножение, деление) над числами целыми и дробными, отвлеченными [?] и именованными [?];
• признаки делимости на некоторые простые числа;
• учение о пропорциях и о его практическом применении в некоторых задачах (правила: тройное, процентов, учета векселей, товарищества и др.);
• возвышение в степень и извлечение квадратных и кубичных корней.

К  высшей арифметике относится исследование общих свойств чисел, учение о рядах и др.

Выделяют также прикладную (коммерческую) арифметику, занимающуюся вычислением рентных, лотерейных, страховых, эмеритальных, пенсионных, арбитражных и других таблиц.

Разделы страницы о числах, арифметических операциях с ними и их интересных свойствах:

• Обозначения чисел
• Школьная арифметика
• Высшая арифметика
• Теория чисел
• Прикладная арифметика
• Библиография по арифметике

Если вы любите увлекательнейшую теорию чисел - читайте также об истории решения Великой теоремы Ферма.

Обозначения чисел

Современные цифры называются "арабскими", хотя являются по происхождению индийскими, причём, и в Индии, и в арабских странах они имеют несколько другую форму.

Римские цифры в Юникоде: Ⅰ (1), Ⅱ (2), Ⅲ (3), Ⅳ (4), Ⅴ (5), Ⅵ (6), Ⅶ (7), Ⅷ (8), Ⅸ (9), Ⅹ (10), Ⅺ (11), Ⅻ (12), Ⅼ (50), Ⅽ (100), Ⅾ (500?), Ⅿ (1000).

Школьная арифметика

Арифметика (греч. arithmetika, от arithmys - число) ["числительница" - у М.Ломоносова], - наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними. Владение достаточно развитым понятием натурального числа и умение производить действия с числами необходимы для практической и культурной деятельности человека. Поэтому арифметика является элементом дошкольного воспитания детей и обязательным предметом школьной программы. С помощью натуральных чисел конструируются многие математические понятия (например, основное понятие математического анализа - действительное число). В связи с этим арифметика является одной из основных математических наук. Когда делается упор на логический анализ понятия числа, то иногда употребляют термин теоретическая арифметика. Арифметика тесно связана с алгеброй, в которой, в частности, изучаются действия над числами без учёта их индивидуальных свойств. Индивидуальные свойства целых чисел составляют предмет теории чисел. Существенную роль в образовании понятия бесконечного натурального ряда чисел сыграл "Псаммит" Архимеда (3 в. до н. э.), в котором доказывается возможность именовать и обозначать сколь угодно большие числа. Сочинения Архимеда свидетельствуют о довольно высоком искусстве в получении приближённых значений искомых величин: извлечение корня из многозначных чисел, нахождение рациональных приближений для иррациональных чисел, например: [также хорошее приближение: 22/7] ... Впервые (в 1427 г.) подробно описал систему десятичных дробей и правила действий над ними аль-Каши. Запись десятичных дробей, по существу совпадающая с современной, встречается в сочинениях С. Стевина в 1585 г. и с этого времени получает повсеместное распространение. К той же эпохе относится изобретение логарифмов в начале 17 в. Дж. Непером. В начале 18 в. приёмы выполнения и записи вычислений приобретают современную форму... (Большая советская энциклопедия)

• .

Высшая арифметика

Разложение на множители и простые числа

• .

Сравнения

• .

Квадратичные вычеты

• .

Непрерывные дроби

Дроби в Юникоде: ⅟ ¹ ² ³ ½ ⅓ ⅔ ¼ ¾ ⅕ ⅖ ⅗ ⅘ ⅙ ⅚ ⅐ ⅛ ⅜ ⅝ ⅞ ⅑ ⅒ .

• .

Суммы квадратов

• .

Квадратичные формы

• .

Теория чисел

Теорию чисел иногда включают в высшую алгебру.

Труды по теории чисел

• Труды по теории чисел. К.Ф.Гаусс.
• Лекции по теории чисел.
• Высшая арифметика. Введение в теорию чисел. Г. Дэвенпорт.

Порталы и статьи о свойствах чисел

• AboutNumber.ru - Интересная информация о свойствах и характеристиках чисел Все делители числа. Простые и числа Фибоначчи. Математические значения. Системы счисления. Число прописью. Разные интересности.

Диофантовы уравнения и их решение

Диофантовыми уравнениями называют уравнения с целыми коэффициентами, для которых требуется найти целочисленные (или натуральные) решения. При этом количество неизвестных в уравнении должно быть не менее двух. Своё название уравнения получили в честь выдающегося античного математика Диофанта Александрийского («отец алгебры», живший предположительно в III веке н. э. [в конце эпохи Древнего мира]), который, как считается, первым систематически изучал неопределённые уравнения и описывал методы их решения. Все сохранившиеся записи собраны в книгу «Арифметика». Диофант первым среди античных учёных предложил развитую математическую символику, которая позволяла формулировать полученные им результаты в достаточно компактном виде. Диофант пытался ответить на следующий вопрос: Дано уравнение с целыми коффициентами. Имеет ли оно целые решения? Нахождение целочисленных решений алгебраических уравнений с 3-мя неизвестными [у самого Диофанта были и с 3-мя неизвестными] в наши дни называется обычно диофантовым анализом. В прошлые столетия такой анализ допускал использование в качестве переменных и рациональные дроби, однако сейчас он ограничивается только целыми числами. Другое, более точное определение: диофантовы уранения - алгебраические уравнения или их системы с целыми коэффициентами, имеющие число неизвестных, превосходящее число уравнений, и у которых разыскиваются целые или рациональные [простые дроби] решения. Примеры диофантовых уранений: ax + by = c, x2 + y2 = d2, x3·8 - x2·16 = x3·1 (как на приведённой иллюстрации). После Диофанта схожим изучение неопределённых уравнений занимались индусские математики, начиная примерно с пятого века [через 200 лет]. В Европе решением неопределённых уравнений занимались практически все крупные алгебраисты своего времени: Леонардо Фибоначчи (ок.1170 — 1250 гг.) [почти через тысячелете после Диофанта], Франсуа Виет (1540—1603 гг.), Симон Стевин (ок. 1549—1620 гг.) [оба - через 400 лет после Фибоначчи]. Проблема решения диофантовых уравнений в целых числах является решённой до конца для уравнений с одним неизвестным, а также для уравнений первой и второй степени с двумя неизвестными.

• Квадратные уравнения. Диофант.
• Диофантовы уравнения. Халецкий Андрей Викторович, Черкас Леонид Антонович [Word Doc, 145 K]
• Решение Диофантовых уравнений. Уравнение ax + by = c. Уравнение x²+y² = d²
• А. А. Болибрух. Проблемы Гильберта (100 лет спустя). Десятая проблема Гильберта: диофантовы уравнения.

Свойства и закономерности простых и натуральных чисел

Также смотрите страницу Великие проблемы математики, раздел по теории чисел и гипотезе Римана - возможной закономерности распределения простых чисел в бесконечном ряду натуральных чисел.

Проблема Гольдбаха

Любое четное число больше 2 можно представить в виде суммы двух простых чисел (1742 г.), например: 10 = 7 + 3 = 5 + 5 [и количество таких комбинаций можно назвать валентностью этого четного числа].

Другая формулировка утверждения Гольдбаха, немного менее известная, — что любое нечетное число, большее или равное 9 [= 1+3+5 = 3+3+3], можно представить в виде суммы трех простых чисел, например, 13 = 7 + 3 + 3 = 5 + 5 + 3 [да - это прямое следствие первой гипотезы].

Самые простые математические утверждения иногда бывает сложнее всего доказать - и изумительные гипотезы Гольдбаха до сих пор не доказаны. [может быть, мезоны, состоящие из 2 кварков (1/3+2/3) - чётные числа, а барионы, состоящие из 3 (1/3 + 1/3 + 1/3) - нечетные? :) ]

Источники:

• Проблема Гольдбаха (Элементы. "Природа науки").

Неожиданное в свойствах простых чисел

Список интересных фактов в операциях над простыми числами:

• Если 111 111 111 умножить на 111 111 111, то получится 12345678987654321.

Статьи энтузиастов по решению проблем простых чисел

Статьи Белотелова В.А. (г. Заволжье):

• Проблема Гольдбаха. Решение первой и второй проблемы Ландау [Zip 330К]. Проблема Гольдбаха (ПГ) и Вторая проблема Ландау (ПЛ2) – задачи родственные. Но за решение Проблемы Гольдбаха премия обещана, а за решение Второй проблемы Ландау - нет. Для доказательства ПГ и ПЛ2 требуется знание закона распределения простых чисел в ряду натуральных чисел (ЗРПЧ), и знание алгоритма решения Диофантовых уравнений (АРДУ).
• Алгоритм решения Диофантовых уравнений [ZIP 260К]. Статья была представлена на X Всероссийском симпозиуме по прикладной и промышленной математике, Санкт-Петербург, 19 мая 2009 г. В статье затронуты вопросы: 1) Диофантовы уравнения. 2) Великая теорема Ферма. 3) Уранение Пелля. 4) Поиск Пифагоровых троек. 5) Решение уравнения Каталана. 6) Гипотеза Биля.
• Признак сходимости Диофантовых уравнений. Еще одна работа В.А.Белотелова
• Закономерность распределения простых чисел в ряду натуральных чисел [Zip 180К].
• О формулах простых чисел [Zip 28К]. Автор приходит к выводу: формул простых чисел не существует.

Статьи по манипуляциям с натуральными числами

Интересные сетевые статьи и ресурсы о свойствах натуральных чисел и их рядов:

• Магические квадраты и палиндромы от Георгия Александрова.
• Математический принцип деления целого (теория Троичности). Как и в исследованиях Корнеева, особую роль в теории Андрея Ткаченко отводится сверхсовершенному числу 24, которое, действительно, обладает уникальными математическими свойствами. Это число имеет 7 делителей (1; 2; 3; 4; 6; 8; 12), сумма которых равна 36, что в 1,5 раза больше самого числа 24, восьмым делителем является само число 24. Количество делителей составляют октаву, а сумма восьми делителей 1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60. Если учесть, что нумерологический период чисел Фибоначчи равен 24, а числа 12 и 60 являются важнейшими числовыми характеристиками додекаэдра (12 граней и 60 плоских углов на его поверхности), то это поднимает наш интерес к числу 24.

Свойства особых иррациональных и трансцендентных чисел (пи, e, фи)

Как известно из геометрии, общею мерою двух отрезков прямой (или двух углов, двух дуг одинакового радиуса, вообще двух значений одной и той же величины), называется такое значение этой величины, которое в каждом из них содержится целое число раз без остатка. Тем не менее, в геометрии утверждается, что могут быть такие 2 отрезка, которые не имеют общей меры, например, сторона квадрата и его диагональ. Числа целые, дробные, десятичные конечные и десятичные периодические носят общее название рациональных чисел; десятичные бесконечные дроби непериодические называются иррациональными числами.

Трансцендентные числа - это числа (вещественные или комплексные), которые не могут быть корнями никакого многочлена с целыми коэффициентами. Например,такие важнейшие константы анализа, как π и e, являются трансцендентными, а √2 не является, поскольку это корень многочлена x²−2.

Главные [а есть другие?] математические константы:

• Число "пи" (выражает отношение окружности к диаметру): π = 3,1415926536... или около 3,14
• Число "е" (основание натуральных логарифмов): e ~2,72?
• Число Фибоначчи (определяет "золотое сечение"): φ ~2,5?

Константы (постоянные числа) имеются или могут иметься во всех науках - как естественных, так и гуманитарных - психологии, лингвистике, истории. Познакомьтесь, например, с физическими константами. Даже, возможно, в философии когда-нибудь откроют великие философские постоянные. Впрочем, не исключено, что ими окажутся как раз наши матконстанты, получив, таким образом, одухотворённость.

Взаимосвязь между базовыми математическими постоянными

Путём хитрых преобразований и операций получены следующие любопытные результаты (источник - статья "Постоянная Гельфонда" в Википедии):

• (e^π)ⁱ = -1
• e^π - π ≈ 20

Иррациональное число Фидия (Φ) от чисел Фибоначчи - основа "золотого сечения"

Знаменитое "Золотое сечение" или Число Фидия φ = (1 + √5) / 2 = 1,61803398874989… является числом, к которому стремится частное от разности соседних чисел Фибоначчи в ряду 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, … , где каждое следующее число есть сумма предыдущих двух чисел, начиная от 0 и 1.

Обратное число, обозначаемое строчной буквой φ = 1 / Φ ≈ 0,61803, откуда следует, что φ = 1 - Φ.

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника. [Интересно. Это поэтому в корне пятёрка?]

Золотое сечение имеет множество замечательных свойств (например, произведение 1,6180339… × 1,6180339... = 2,6180339…) но, кроме того, ему приписывают и многие вымышленные свойства. А вот не менее невероятные, но реальные удивительные свойства числа Фидия:

• Φ — иррациональное алгебраическое число (мера иррациональности Φ равна 2), положительное решение квадратного уравнения x² - x - 1 = 0, откуда, в частности, следуют соотношения:
  • Φ² - Φ = 1,
  • Φ · (Φ - 1) = 1.
Φ представляется через тригонометрические функции:
• Φ = 2cos(π/5) = 2cos36°,
• Φ = 2sin(3pi;/10) = 2sin54°.
• А при делении пополам угла между диагональю и меньшей стороной прямоугольника с отношением сторон 1:2 по формуле тангенса половинного угла получаем соотношение: 1/Φ = φ = tg(arctg(2)/2) = 2/(1+√(1+2²)) = 2/(1+√5) = (√5-1)/2.
• Φ представляется в виде бесконечной цепочки квадратных корней...
• Также Φ представляется в виде бесконечной цепной дроби...
• Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ = a/b, что и у исходного прямоугольника Φ (a+b)/a.

Ссылки на обзоры и статьи по золотому сечению, числу Фидия и ряду Фибоначчи:

• Вычисление чисел Фибоначчи (Викиучебник).
• Золотое сечение (ВикипедиЯ)
• Числа Фибоначчи. (Элементы. "Природа науки"). Последовательность чисел, каждый член которой равен сумме двух предыдущих, имеет множество любопытных свойств.
• Числа Фибоначчи в природе.
• 5 способов вычисления чисел Фибоначчи: реализация и сравнение (Хабр).
• Глава 9. Числа Фибоначчи. Идеи реализации.

Трансцендентное число π - основа квадратуры круга

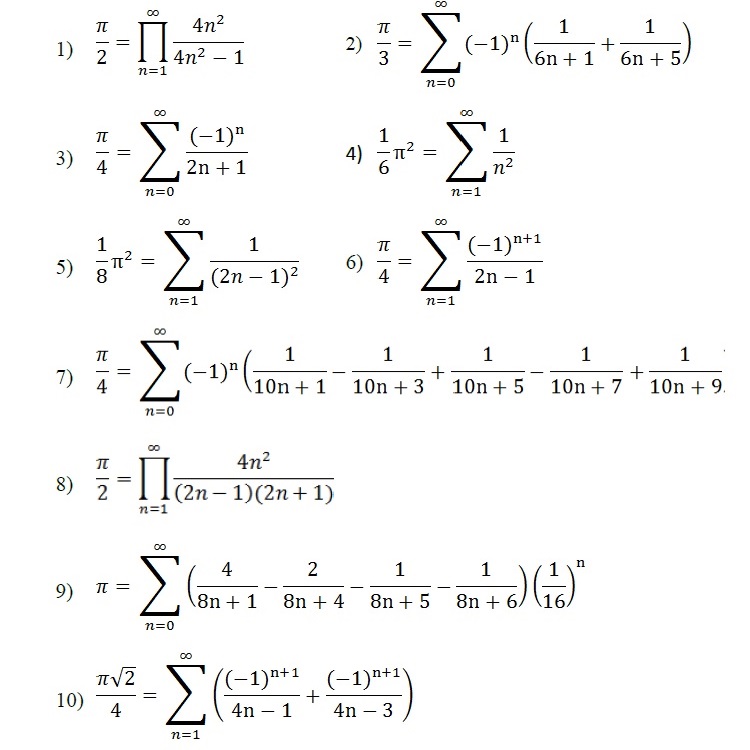
Пи = 3,141 592 654 ... Зона ПИ. (На "Арбузе").

Трансцендентное число e - основа логарифмов

Сетевые ресурсы об иррациональных и трансцендентных числах

Обзоры и сборники статей о свойствах нерациональных и операций с ними чисел:

• Иррациональные числа.
• Теория трансцендентных чисел (Материал из Википедии — свободной энциклопедии)

Прикладная арифметика

Коммерческие приложения арифметики.

• .

Библиография по арифметике

• Диофант. Арифметика и книга о многоугольных числах. М.: Наука, 1974.

---

© «Сайт Игоря Гаршина», 2002, 2005. Автор и владелец - Игорь Константинович Гаршин (см. резюме). Пишите письма ().

Страница обновлена 22.03.2024