|
|
Главная |
|
|
Пишите |
|
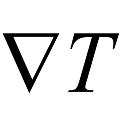
Хорошая теория – самая практичная вещь на свете. Математический анализ — совокупность разделов математики, посвященных исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей трактовке к анализу следует отнести и функциональный анализ вместе с теорией интеграла Лебега, комплексный анализ (теория функций комплексного переменного - ТФКП), изучающий функции, заданные на комплексной плоскости, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, а также вариационное исчисление. |
В учебном процессе к анализу относят:
При этом элементы функционального анализа и теории интеграла Лебега даются факультативно, а ТФКП, вариационное исчисление, теория дифференциальных уравнений читаются отдельными курсами. Строгость изложения следует образцам конца XIX века и, в частности, использует наивную теорию множеств.
В математический анализ для высшего образования входят теории пределов, функций, рядов, дифференциальных уравнений; аналитическая геометрия, дифференциальная геометрия, топология и др. Курс анализа, читаемый в университетах РФ, примерно соответствует англо-американскому курсу «Calculus». (Из Википедии и других источников)
Что сегодня мы называем анализом? Немного логики и теории множеств, доля аксиоматической теории полных упорядоченных полей, аналитической геометрии и топологии, причем последней как в "общем" смысле (пределы и непрерывные функции), так и в алгебраическом (ориентация). К этому нужно еще добавить собственно теорию функций действительного переменного (дифференцирование), оперирование комбинаторными символами, называемое формальным интегрированием, азы теории меры в низшей размерности, кое-что из дифференциальной геометрии, основы классического анализа тригонометрических, показательных и логарифмических функций. Наконец, в зависимости от объема книги и наклонностей автора, домашняя стряпня из дифференциальных уравнений, элементарная механика и приложения в небольшом ассортименте. По каждому из этих предметов нелегко написать хорошую книгу; смешать же их невозможно.
Разделы страницы об матанализе:
Интегральное исчисление возникло из потребности создать общий метод разыскания площадей, объёмов и центров тяжести. В зародышевой форме такой метод применялся еще Архимедом.
Систематическое развитие он получил в XVII веке в работах Кавальери, Торричелли, Ферма, Паскаля и других ученых. В 1659 году Барроу установил связь между задачами определения площади и касательной. А в 70-х годах XVII века Ньютон и Лейбниц стали рассматривать эту связь в отрыве от прикладной геометрии. Так было установлено отношение между интегральным и дифференциальным исчислением.
Векторный анализ — раздел математики, изучающий вещественный анализ векторов в двух или более измерениях. Методы векторного анализа находят наибольшее применение в физике и инженерии.
Векторный анализ изучает векторные поля — функции из n-мерного векторного пространства в m-мерное — и скалярные поля — функции из n-мерного векторного пространства в множество скаляров.
Важнейшие операции векторного анализа — градиент, ротор, дивергенция. Четвёртая операция, оператор Лапласа, является комбинацией градиента и дивергенции. Среди наиболее важных теорем векторного анализа — теорема Стокса, частными случаями общей современной формулировки которой являются формула Кельвина-Стокса и формула Остроградского-Гаусса.
Многие из результатов векторного анализа рассматриваются как частные случаи результатов из дифференциальной геометрии.

Вариационное исчисление - часть математического анализа, занимающаяся исследованием возможного изменения функций при возможном изменении независимого переменного. Открыто Лагранжем и впервые применено к отысканию max и min определенных интегралов. (Энциклопедический словарь Ф. Павленкова) Вариационное исчисление - раздел математики, обобщающий элементарную теорию экстремума функций. В вариационном исчислении речь идет об экстремуме функционалов - величин, зависящих от выбора одной или нескольких функций f1, f2, . . . fm, которые играют для функционала F[f1, f2, . . . fm] роль аргументов.
Вариационное исчисление — это раздел математики, в котором изучаются вариации функционалов.
Самая типичная задача вариационного исчисления состоит в том, чтобы найти функцию,
на которой функционал достигает экстремального значения.
Методы вариационного исчисления широко применяются в различных областях математики,
в дифференциальной геометрии с их помощью ищут геодезические и минимальные поверхности.
|
Ключевые слова для поиска сведений по высшей математике и математическому анализу:
На русском языке: математический анализ, матанализ, высшая математика,
исследование функций многих переменных, изучение бесконечно малых и бесконечно больших чисел,
вычисление производных, нахождение пределов, степенные ряды,
интегрирование дифференциалов, интегральное исчисление, интегралы,
функциональные уравнения, ряжы Фурье, комплексные переменные, асимптотические методы,
наивная теория множеств, нелинейные колебания, теория устойчивости,
аналитическая геометрия, векторная алгебра, алгебраическая топология, ряды Лебега;
На английском языке: mathematic analysis.
|
|
|