|
|
Главная |
|
|
Пишите |
|
|
Позволительно надеяться, что установившийся прискорбный разрыв между математикой и ее жизненными приложениями, неизбежный во времена критических ревизий, сменится эрой более тесного единения." (Р. Курант, Г. Роббинс. Что такое математика?) |
Разделы страницы об истории математики:
|
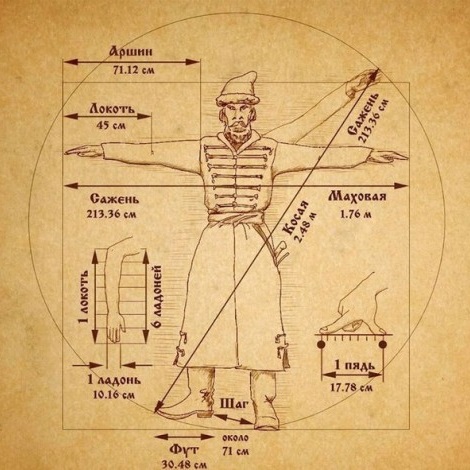
Древние и старинные русские меры длины (от меньших к большим):
То есть, основные русские меры длины это: 1) пядь, 2) аршин (4 пяди), 3) сажень (3 аршина), 4) верста (500 саженей). |
Античные меры веса (во всяком случае, древнегреческие) были основаы на древнейшей вавилонской (по происхождению - шумерской, или даже "допотопной") системы мер. Основными весовыми мерами Месопотамии были билту, ману, шиклу; в Древней Греции - талант, мина, статер; в Древней Иудее - киккар, мане, сикль, соответственно.
Это единообразие в измерении веса обусловлено международной торговлей. А вот при измерении расстояния такого однообразия не наблюдается. Даже мера "локоть" была в разных странах Древнего мира разной:
Шестидесятиричная (точнее - шестерично-десятиричная) математико-астрономическая система. [Может у них и координатная система была полярной?]
Двадцатиричная система, позиционная (с нулем).
Период чисел и дробей. Изобретение нуля индийцами и майя.
Делай великое, не обещая великого.
Начало - половина целого.
Не гоняйся за счастьем: оно всегда находится в тебе самом.
Великая наука жить счастливо состоит в том, чтобы жить только в настоящем.
Омывай полученную обиду не в крови, а в Лете, реке забвения.
Человек, оказавшийся в плену своих страстей, свободным быть не может.
Жизнь подобна игрищам: иные приходят на них состязаться, иные - торговать, а самые счастливые - смотреть.
Берегите слезы ваших детей, дабы они могли проливать их на вашей могиле.
Пифагор
Пифагор Самосский, сын Мнесарха–камнереза (ок. 570 - 500 до н.э.) - греческий философ и математик. Был строгим вегетарианцем. В Кротоне (Италия) основал этико-религиозное пифагорийское товарищество, получившее большое распространение, целью которого было нравственное обновление и очищение религиозных воззрений. Лидер аскетической общины, в которую входили как мужчины, так и женщины, считавшие Пифагора гиперборейским Аполлоном. Философия представляет попытку свести все явления к числовым отношениям и рассматривать числа как непреходящую сущность вещей.
Пифагору приписывают сочинения по геометрии (теорема Пифагора), теории чисел, астрономии, определение основных музыкальных интервалов (считал, что небесные тела подчиняются аналогичным законам гармонии - концепция "музыки сфер"). Пифагорейцы признавали бессмертие душ и их постепенное очищение посредством переселения. Принимали шарообразность Земли и ее движение вокруг центрального огня, источника света и тепла.
Аристарх Самосский (Aristarchos Samios) (кон. 4 в. - 1-я пол. 3 в. до н. э.) - древнегреческий астроном. В сочинении "Псаммит" Архимед сообщает краткие сведения об астрономической системе Аристарха Самосского, изложенной в не дошедшем до нас его сочинении. Как и Птолемей, Аристарх Самосский считал, что движения планет, Земли и Луны совершаются внутри сферы неподвижных звёзд, которая, по представлению Аристарха Самосского, неподвижна, как и Солнце, находящееся в её центре [это уже не по Птолемею]. Земля движется по кругу, в центре которого находится Солнце.
Построения Аристарха Самосского - высшее достижение древней гелиоцентрической доктрины;
их смелость навлекла на автора обвинение в богоотступничестве, и он вынужден был покинуть Афины.
Единственный сохранившийся небольшой по объёму труд Аристарха Самосского "О размерах и расстояниях Солнца и Луны"
был впервые издан в 1688 в Оксфорде на языке оригинала.
Лит: Берри А., Краткая история астрономии, пер. с англ., 2 изд., М.—Л., 1946.
Птолемей (Ptolemaios) Клавдий (2 в.) - древнегреческий учёный [астроном и географ]. Разработал геоцентрическую систему мира, согласно которой все видимые движения небесных светил объяснялись их движением (часто очень сложным) вокруг неподвижной Земли. [Почему эта дремучая идея разработана после гелиоцентрической системы Аристарха Самосского??] Большую часть жизни он провёл в Александрии, где в 127—151 производил астрономические наблюдения; умер он около 168 г.
Основное сочинение Птолемея по астрономии — «Великое математическое построение астрономии в 13 книгах», (араб. «Альмагест». До появления книги «Об обращениях небесных сфер» Николая Коперника «Альмагест» оставался непревзойдённым образцом изложения всей совокупности астрономических знаний. Исключительно велико было практическое значение этой работы для мореплавания и определения географических координат, В «Альмагесте» впервые законы видимых движении небесных тел были установлены настолько, что стало возможным предвычисление их положений. В начале 17 в., во время борьбы за утверждение гелиоцентрической системы мира, отношение к сочинению Птолемей резко изменилось, так как в нем стали прежде всего видеть опору геоцентрических взглядов; в это же время, после появления таблиц Коперника и особенно Иоганна Кеплера этот труд потерял свое практическое значение.
Большой известностью пользовалось и другое сочинение Птолемея — «Руководство по географии» (8 книг).
В нём дана полная, хорошо систематизированная сводка географических знаний древних (основанная на сообщениях путешественников).
Птолемей дал координаты 8000 пунктов (от Скандинавии до верховьев Нила и от Атлантического океана до Индокитая).
К трактату приложены одна общая и 26 специальных карт земной поверхности.
Соч.: Opera quae exstant omnia, ed. J. L. Heiberg, v. 1—2, Lpz., 1898—1907; Geographia. E codicibus recongnovit, C. Mullerus, v. 1—2, Parisis, 1883—1901.
Не меньший интерес представляют и другие сочинения Птолемея (оптика, история...), некоторые из которых сохранились.
Эратосфен (II век) первый поставил задачу определения простых чисел.

Диофант Александрийский (3-й век) - древнегреческий математик. В основном труде "Арифметика" (сохранились 6 книг из 13) [ее любил штудировать Пьер Ферма] дал решение задач, приводящихся к т.н. диофантовым уравнениям (решения которых только в целых числах), и впервые ввел буквенную символику в алгебру. В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней. При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные. Рассмотрим одну из его задач. «Найти два числа, зная, что из сумма равна 20, а произведение 96». Диофант рассуждает следующим образом: Из условия задачи вытекает, что искомые числа не равны, так как если бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, то есть 10 + х, другое же меньше, то есть 10 – х. Разность между ними 2х. Отсюда уравнение (10 + х)(10 - х) = 96 или Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = - 2 для Диофанта не существует, так как греческая математика знала только положительные числа. |
Имя Абу Али ал Хусейн ибн Абдаллах ибн ал-Хасан Али ибн Сины (в европейской традиции - Авиценны) (ок.980 - 1037) традиционно связывают прежде всего с медициной и философией...
Ключевые слова для поиска сведений о великих математиках и математических открытиях:
На русском языке: история математики, великие математики античности, математические открытия, древние меры,
единицы измерения в Древнем мире, древнейшие математические системы, диофантовы уравнения,
Пифагор Самосский, Аристарх, Птолемей, Архимед, Эратосфен, Диофант Александрийский, Ипатия, Абу Рейхан Бируни,
Авиценна, король математики Эйлер, Гаусс, Галуа, Ньютон, Лежандр, Дирихле, Гольдбах, Гилберт, Танияма, Минковский;
На английском языке: mathematical discovery.
|
|
|